Oligopolio calcolo delle curve di reazione. L’argomento è uno di quelli che provoca i “capelli dritti” a tutti i nostri studenti e il motivo è semplice: viene spiegato male. C’è come un gusto, nei nostri docenti titolati di cattedra, nel rendere non comprensibile la materia (microeconomia). La tecnica utilizzata per complicare il concetto è la matematica.

Cosa ci faccia la matematica in economia non si sa.

La vecchia microeconomia è affogata nella matematica.

La nuova microeconomia discute a tu per tu con la sociologia dei consumi e la psicologia comportamentale.

Gli attuali quadri nella docenza tradizionale, in particolare per microeconomia, sono “vecchi” non come età, ma per ragionamento e attitudine alla spiegazione. I docenti più giovani sono spesso (quasi sempre) peggio dei più maturi perchè non rispondono agli studenti nelle loro richieste utilizzando la loro cattedra come trampolino di lancio nella carriera personale anzichè servizio alla cultura.

Chiarito il pessimo contesto dove si colloca un argomento da “prendere con le pinze” come l’oligopolio, che si entri nel dettaglio.

Il concetto di “curva di reazione” è noto (lo si considera scontato a questo livello d’approfondimento). Ovviamente le curve sono 2 perchè s’ipotizzano 2 aziende in attività. Quello che c’interessa è come si calcolano le curve di reazione.

Sia data una curva di domanda (inversa) come p = 100 – Q

Essendo le 2 imprese uguali, sostengono CF (costi fissi) per 100 e un costo marginale di 10

Con questi dati si calcolino le 2 curve di reazione (o anche chiamate di risposta ottima).

Si segua la presente tabella di marcia per l’oligopolio calcolo delle curve di reazione:

1 – la curva di domanda (D), in questi caso è sempre espressa in forma inversa;

2 – si cerchi il Profitto (indicato solitamente come P greco) di uno degli operatori sapendo che è uguale al prezzo per la quantità (qa). In questo caso il Profitto è certamente p x qa meno i costi sostenuti (fissi e variabili/marginale). Con queste specifiche il Profitto è

Profitto = p x qa – 100 (CF) – 10qa

3 – sapendo che si tratta di Oligopolio, ovvero ci sono 2 produzioni pari a qa e qb, la funzione inversa della D si può scrivere come p = 100 – qa – qb;

4 – con questi dati la funzione della D inversa va moltiplicata per la quantità A meno i costi che sostiene per produrre, quindi:

Ricavo Totale, RT = (100 – qa -qb) qa – 100 – 10qa

per leggere quest’ultima funzione abbiamo il mercato, spezzato tra 2 produzioni è posto in relazione con 1 produttore (qa) a cui togliamo i costi di produzione.

Sviluppando la funzione si perviene a RT = 90qa- qa al quadrato – qaqb – 100

5 – Per calcolare le curva di reazione serve la derivata parziale, rispetto al primo produttore (successivamente sarà anche per l’altro) della funzione appena calcolata. Si rammenta che la derivata del Ricavo totale è il Ricavo marginale. Noi stiamo cercando l’equiparazione tra Ricavo Marginale e il costo marginale (che ci è già stato fornito in 10). Basta ricordare il monopolio e il suo equilibrio, ovvero RM = CM, quindi ricavo marginale = costo marginale.

Se questo è vero (replica di quanto già sappiamo dal monopolio) la derivata parziale rispetto a qa della funziona sopra calcolata è pari a 90 – 2qa – qbqa.

Il ricavo marginale è quindi pari a RM = 90 – 2qa – qbqa

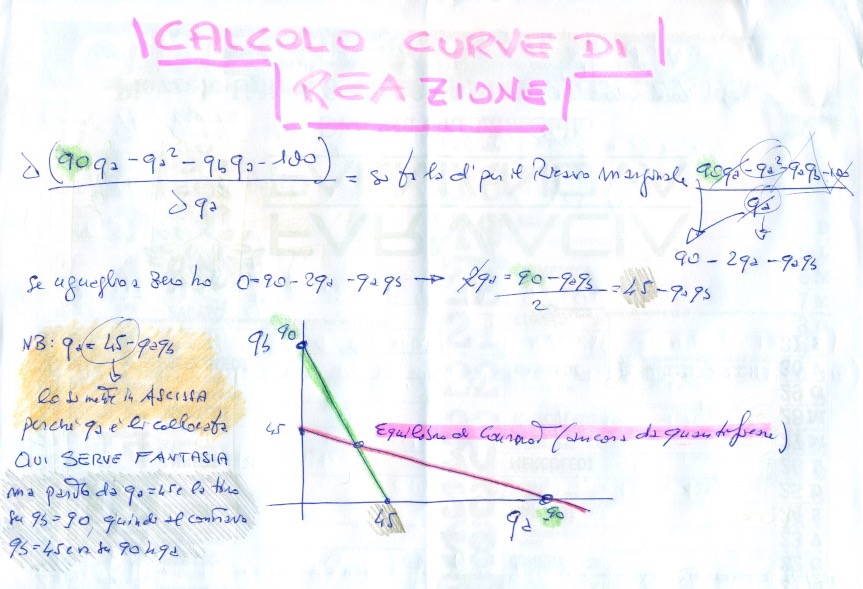
6 – Eguagliando a zero la funzione del RM ovvero 0 = 90 – 2qa – qbqa è possibile risolverla in 45 – qbqa

7 – E’ stata così ottenuta la curva di reazione per cui:

il produttore “a” avrà una curva di reazione con intercette pari a 90 in ordinata e 45 in ascissa;
mentre per l’altro produttore la curva di reazione avrà in ordinata 45 e in ascissa 90;
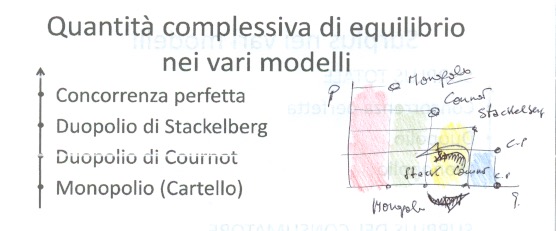
il punto di contatto tra le 2 curve di reazione rappresenta il punto d’equilibrio detto punto di Cournot che va calcolato, ma questa è un’altra avventura a seguire.

Oligopolio calcolo delle curve di reazione termina qui.