La funzione d’utilità è pari a U (x, y) = x al quadrato y.
Da questa funzione se ne estragga il SMS (saggio marginale di sostituzione).
Con tale calcolo si entra nel nervo scoperto della microeconomia: qui tutti soffrono!
S’anticipano 3 considerazioni:
- il SMS è sempre la Y sull’ X quindi assume la forma di un Y/X
- il calcolo del saggio marginale impone una cerimoniosità che transita attraverso le derivate;
- il SMS ci serve, se posto in collegamento al vincolo di bilancio con una parentesi graffa, per definire le quantità consumate del bene x e di y nel paniere d’equilibrio. (Questo terzo passaggio non viene qui calcolato).
Stabiliti i comandamenti iniziali, si proceda con le derivate attraverso 4 passaggi:
PASSO 1: Il SMS è pari al rapporto tra l’utilità marginale di X con l’utilità marginale di y
PASSO 2: Per risolvere questo rapporto tra utilità marginale serve la derivata parziale motivo per cui:
al numeratore: la derivata parziale di x al quadrato ed y / (fratto) la derivata parziale di x
ad denominatore: la derivata parziale di x al quadrato e la y/ (fratto) la derivata parziale di y
PASSO 3:
al numeratore: applicando la derivata, quell’x al quadrato diventa 2x mentre y non è interessata alla derivata parziale con x. Ne consegue che emerge un 2xy sopra (numeratore) che si semplifica con la x (del denominatore) per cui resta 2y
al denominatore: applicando la derivata, compare ancora x al quadrato con la y ma stavolta ponendo il tutto in relazione con la derivata parziale di y. X al quadrato resta così com’è. La Y “prende” l’esponente 1 della sua elevazione a potenza lasciando la y con esponente zero ovvero pari a 1. Ne consegue che resta x al quadrato e 1 che moltiplica 1 ovvero x al quadrato.
PASSO 4
La parte complicata di questo denominatore è trovarsi un x al quadrato fratto y.
Ci si trova ora con una triplice frazione che va trattata in questo modo:
2y/x al quadrato/fratto a sua volta y
La risolviamo moltiplicando 2y per y fratto x al quadrato.
L’y al quadrato e la x al quadrato si semplificano perdendo entrambi l’elevazione a potenza.
La conclusione è 2y/x: questo è il saggio marginale di sostituzione.
La funzione d’utilità è stata risolta.

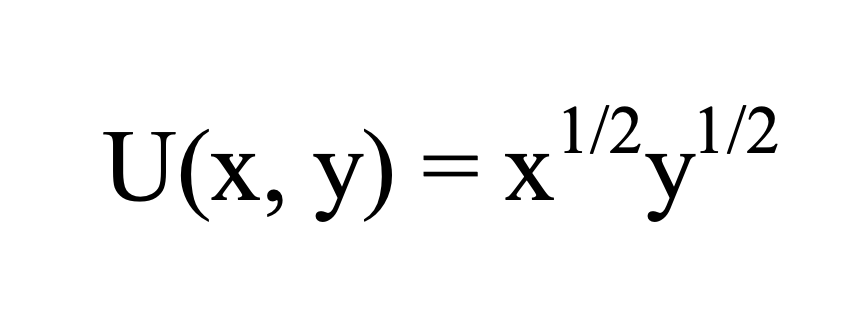
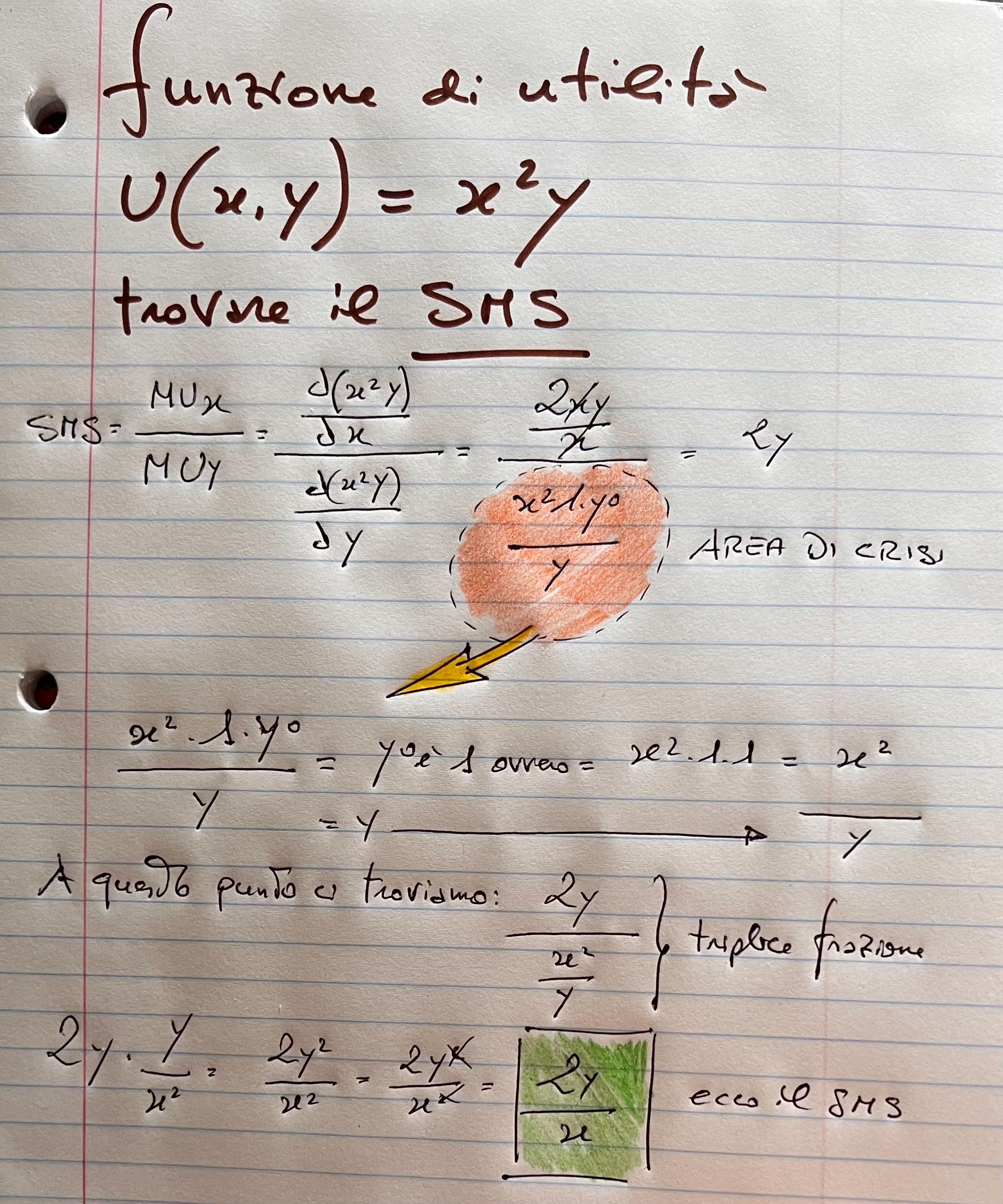





Scrivi un commento