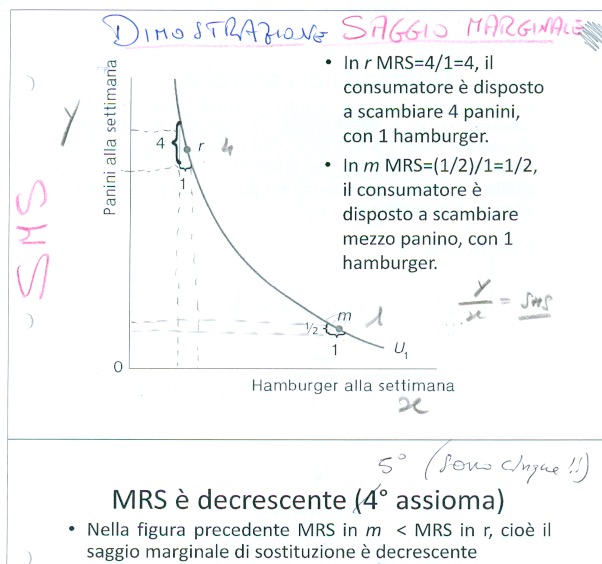
Saggio marginale di sostituzione, il calcolo. Il motivo per cui si scrivono questi appunti è che c’è un problema. S’osservi come si presenta il calcolo in questa immagine:
Ebbene la letterale applicazione di quest’impostazione impone un errore. Il concetto va spiegato con un esempio pratico.
Sia data l’Utilità (U) di x,y pari a x al quadrato, y.
Applicando quanto sopra indicato emerge un saggio marginale di sostituzione pari a 2y/x al quadrato ma è errato. Questo è il guaio.
In realtà quanto mostrato va compreso in altro modo (ecco perchè lo studio della micro è oggettivamente complesso per quanto potremmo renderlo decisamente più chiaro!)
La corretta interpretazione è la seguente: prendere l’Utilità derivando solo la x a numeratore, quindi prendere l’Utilità derivando solo la y a denominatore.
In termini pratici avviene che: 2xy/x al quadrato che moltiplica 1. Ovviamente si veda la grafica predisposta qui sotto.
Con un 2xy fratto x al quadrato che moltiplica 1, si semplificano le x per cui il saggio marginale di sostituzione è pari a 2y/x.
Per una maggiore chiarezza del concetto s’osservi quanto indicato qui di seguito su foglio allegato.
Il punto critico è quell’1 a denominatore che potrebbe confondere, ovvero quanto corrisponde alla y ma è facilmente spiegabile. Si tratta della derivata della y. Le regole di derivazione spiegano che quando un valore ha come elevazione a potenza l’unità la sua derivata è pari a 1.
Come si nota dal secondo allegato qui presente, appositamente è stata evidenziata in giallo la “y” che rappresenta una delle “pietre dello scandalo” di questo conteggio. In questo modo è possibile seguirne l’evoluzione fino a diventare 1.
CONCLUSIONI








Scrivi un commento