Isoquanto questo birichino giunge alla sua puntata numero 3. In quest’occasione l’approfondimento riguarda la connessione tra le funzione di produzione e la scala della produttività.
Come noto la produttività può essere sviluppata con rendimenti di scala di tipo costante, crescente o decrescente, ma qui il ragionamento è come collegarla “ad occhio” alla funzione di produzione.
Le funzioni di produzione possono essere indicate nei seguenti modi:
Q (L;K) = 2 (L+K)
Q (L;K) = L elevato a 1/4 e K elevato a 2/4
Q (L;K) = 2 (LK) elevato a 1/2
Q (L; K) = min (L;2K)
Analizzando il primo caso si ha che la quantità prodotta, in tale funzione di produzione, utilizzando input di Lavoro e Capitale, si sviluppa con 2 unità dell’uno e dell’altro.
Pensandoci bene si tratta di materie prime perfettamente sostitute. In questo caso l’isoquanto, come già spiegato nei precedenti studi già pubblicati, è pari a:
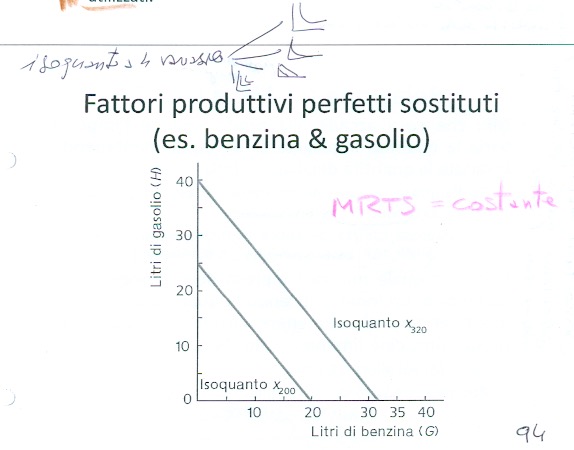
In queste condizioni la produttività è automaticamente COSTANTE
La seconda funzione di produzione si presenta come una Cobb-Douglas perchè sono presenti delle frazioni come esponenti degli input di produzione.
Un’indicazione a frazione degli esponenti può avere tre diversi esiti: uguale, maggiore o minore di 1. E’ gioco forza che se la somma degli esponenti fosse pari a 1 il rendimento è sicuramente COSTANTE.
Ne deriva agevolmente che in caso di somma superiore all’unità il rendimento di scala sarà CRESCENTE o DECRESCENTE nel caso opposto.
Solitamente la Cobb-Douglas piace a tutti gli studenti pur spaventandoli.
Sgombrato il campo dalle funzioni di produzione del tipo Cobb-Douglas c’è quella dove si legge “min” ovvero al minimo. Qui siamo nel campo studiato da Leontiev con rendimenti di scala complementari.
Il connesso isoquanto con Leontiev si presenta come già noto e così rappresentato:

Qui lo studio si complica ma neppure più di tanto.
La sorpresa che è “solitamente” una funzione del tipo Leontiev è con rendimenti di scala COSTANTI.







Scrivi un commento