Calcolo elasticità incrociata in microeconomia. Si tratta del terzo ed ultimo tipo d’elasticità qui studiato dopo quella al prezzo e al reddito.
In analogia a quanto già visto nel caso dell’elasticità al reddito, anche in questo caso c’è da interrogarsi sulla natura dei beni che sono oggetto dell’incrocio sotto esame.
Più che normali o inferiori (come nel caso del reddito) la natura del prodotto per l’incrociata è del tipo:
- beni sostituti;
- beni complementi.
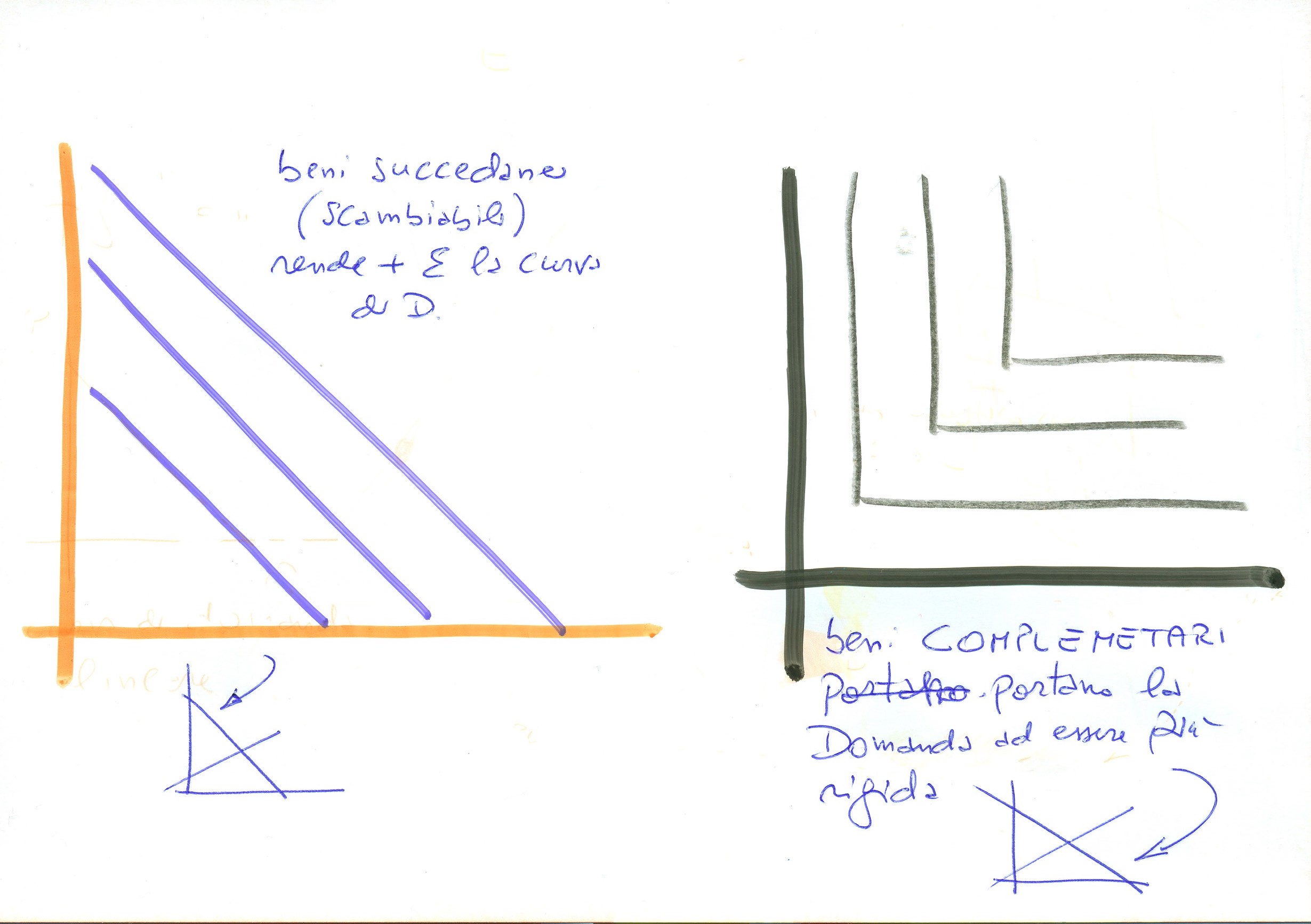
Si rammenta che per sostituiti s’intendono quei prodotti che sono succedanei, il cui consumo è alternativo e concorrente. Quindi the e caffè, riso e pasta. Il consumo di uno riduce o esclude l’altro. In un certo senso sono prodotti concorrenti.
Certamente è gradevole osservare la forma della curva curva di domanda sia nel caso dei succedanei che complementi.
Prima di dedicarsi alla grafica va ricordato come i beni complementi non siano concorrenti ma d’integrazione nel consumo: benzina e autovettura.
Ora abbiamo le carte in regola per discutere d’elasticità incrociata.
Se i beni sono succedanei/sostituiti l’elasticità sarà maggiore di zero.
Nel caso di beni complementi avremo elasticità INFERIORI A ZERO.

Ora il calcolo dell’elasticità incrociata.
Come sempre abbiamo la medesima impostazione (si notino le similitudini). Si tratta della prima parte della formula ora sotto osservazione per le similitudini.
a) elasticità incrociata:

b) elasticità al reddito:
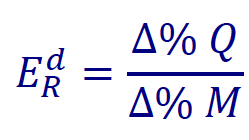
c) elasticità al prezzo:

A tutte queste prime parti della formula, segue inesorabilmente il rapporto tra quanto figura a denominatore traslato a numeratore nel secondo elemento della formula, diviso per la quantità d’equilibrio. Si osservi:
a) nuovamente l’elasticità incrociata, STAVOLTA PERO’ COMPLETA ANCHE DELLA SECONDA PARTE DELLA FORMULA:
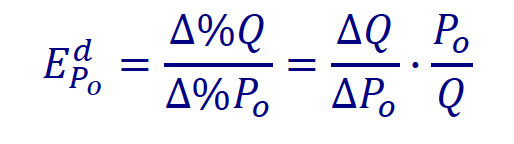
si osservi come a numeratore della seconda parte della formula si trovi il prezzo di uno dei due beni; una caratteristica che ritroviamo in ogni altra formula.
b) ecco di nuovo l’elasticità al reddito PERO’ COMPLETA COME FORMULA ANCHE DELLA SECONDA PARTE:
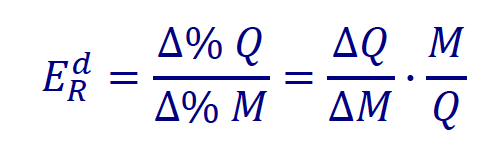
anche qui la M di reddito che si trova al denominatore della prima parte della formula, trasla al numeratore della seconda parte.
c) infine la formula completa dell’elasticità al reddito che rispetta le stesse caratteristiche osservate:

Buon studio cosciente d’aver aiutato gli studenti nel calcolo elasticità.







Scrivi un commento